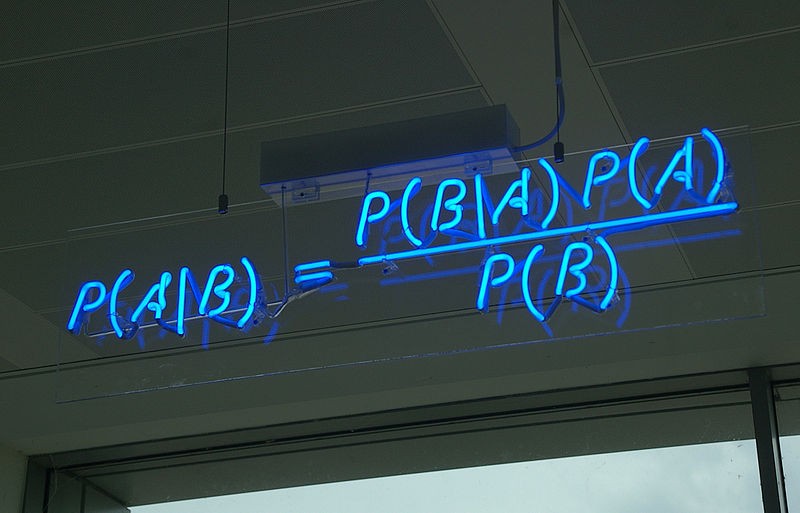Новый метод учета и контроля ядерных материалов

Экономичный метод подтверждения соответствия качества учета и контроля ядерных материалов нормативным статистическим критериям с помощью случайных выборок основан на введении понятия функции состояния системы, комбинаторных правилах ее построения по функциям состояния подсистем и использовании теоремы Байеса.

Процесс учета и контроля ядерных материалов (ЯМ) предусматривает периодическое проведение проверок различных типов. Так, проверяется степень соответствия устройств индикации вмешательства данным, содержащимся в учетной документации (наличие, целостность, оттиск и прочее), согласованность атрибутивных признаков учетных единиц и данных оперативно-технического учета и т.д. Во многих случаях из-за ограничений по временным, технологическим, радиационным и другим факторам проверки приходится проводить выборочно.

Требования к выборочным проверкам содержатся в действующих  нормативных документах по учету и контролю. В качестве критериев наиболее часто применяют показатели величины вероятности P0 и доли дефектных элементов a₀. Используя их, требования к выборочным проверкам можно сформулировать следующим образом: при проведении проверки объем случайной выборки n должен быть таким, чтобы с вероятностью не ниже P₀ можно было исключить наличие в проверяемой системе дефектов в количестве D₀ = a₀ N (N – число элементов в системе) и более.

Метод Джейка

В основе методологии определения объемов выборок в зависимости от размеров системы и количества дефектных элементов, обнаруживаемых в выборке, как правило, лежит метод оценки гипотез, называемый также методом Джейка.

Решение задачи сводится к нахождению наименьшего объема выборки n, содержащей d дефектов, при котором удовлетворяется неравенство:

где w (N, D, n, m) – функция гипергеометрического распределения.

Объем выборок, полученный в результате применения метода Джейка, часто составляет значительную долю от всей совокупности элементов. Однако в ряде случаев (в крупных хранилищах, при жестких ограничениях по возможному числу дефектов и т.д.) затруднительно выполнять не только сплошные проверки, но и выборочные с достаточно большим объемом случайных выборок. В такой ситуации использование метода Джейка для решения проблем учета и контроля ЯМ приводит к рекомендациям, которые не могут быть реализованы на практике.

Бинарная функция состояния системы

Анализ исходных предположений, используемых в методе Джейка, показывает, что в этом методе никак не учитывается одна из важнейших особенностей   проверяемых на практике систем. Она состоит в том, что выборка производится из системы, относительно которой имеется априорная информация, полученная, например, при предыдущих проверках. Наличие такой информации и ее надлежащий учет, вероятно, должны уменьшить объем выборки, необходимой для подтверждения соответствия состояния системы заданным критериям.

Для учета наличия априорной информации разработан математический аппарат, в котором для описания системы используются термин «функция состояния» (ФС) системы. Эта функция – p_N ^(D) – означает вероятность наличия в системе, содержащей N элементов, D дефектов, при этом D может принимать значения D = 0,1,..., N. ФС системы обладает свойством нормировки:

Апостериорная функция состояния системы (ФС после проведения выборочных проверок и регистрации d дефектных элементов в случайной выборке объемом) обозначается как  и вычисляется по известной перед проведением проверок априорной ФС  и результатам случайной выборки с помощью известной в теории вероятности теоремы Байеса:

Далее эта функция называется бинарной функцией состояния системы – БФС.

Характер изменения ФС системы по результатам выборочных проверок иллюстрируется на рисунках 1 и 2. В рассмотренных примерах в системе было 80 элементов, объем выборки составил 13 элементов, из которых все оказались исправными. В первом случае перед проведением выборочных проверок система имела вид «полочки» (рис.1., верхний график), во втором – комбинации «полочки» и «спадающей» экспоненты (рис.2, верхний график).

Рис. 1. БФС в случае ФС типа «полочка»: вверху – ФС системы перед выборочной проверкой, внизу – ФС системы после выборочной проверки

Рис. 2. в случае ФС типа «полочка+экспонента»: вверху – ФС системы перед выборочной проверкой, внизу – ФС системы после выборочной проверки

Апостериорные ФС, приведенные на нижних графиках рисунков 1 и 2, отличаются от априорных большей крутизной и большими значениями ФС в области малых значений переменной D. Это означает, что системы после выборочных проверок оказались в среднем менее «дефектными», поскольку уменьшилась вероятность обнаружить системы с большим количеством дефектных элементов.

Метод БФС

Метод, оперирующей значениями функции состояния системы, был назван методом БФС. Помимо правила нахождения апостериорной ФС (формула 3), он включает в себя модель деградации ФС системы в периоды времени, в течение которых система не проверяется, а также определенные правила композиции, то есть построения ФС системы по известным функциям состояния подсистем (для учета прихода/расхода элементов в системе).

В рамках введенных понятий и перечисленных положений развит математически строгий подход к вычислению объемов выборок, при котором учитываются результаты ранее проводившихся проверок. Объемы выборок, необходимые для подтверждения соответствия учета и контроля заданным критериям, при использовании метода БФС могут оказаться существенно ниже, чем при применении метода Джейка.

В качестве иллюстрации приведем пример нахождения объема выборки методами оценки гипотез и БФС. Пусть система состоит из N = 1000 элементов, P₀ = 0,95, D₀ = 10. Используя формулу 1 (по методу гипотез) и формулу 3 (по методу БФС), находим необходимые объемы выборок (см. таблицу).

Объемы выборок для подтверждения соответствия состояния системы критериям вероятности и доли дефектных элементов

При расчетах методом БФС в качестве априорной информации использовались следующие предположения. Система при первой проверке была проверена выборочным образом, объем выборки составлял n = 258, выборка оказалась бездефектной (d = 0). По результатам первой проверки соответствие состояния системы критериям подтверждено по методу Джейка. В промежутке между первой и второй проверками полное число элементов в системе оставалось неизменным. Число ступеней защиты системы и учетно-контрольной информации равно k=3. Вторая выборочная проверка производилась через интервал времени t, равный половине нормативного времени T между двумя плановыми физическими инвентаризациями (межбалансового периода).

Формула 3 позволяет найти БФС  при любом виде априорной ФС . Если в качестве априорной ФС используется равновероятное распределение дефектных состояний, то есть когда

функцию  обозначим как . Установлено, что рассчитанные по ней объемы выборок совпадают с объемами, определяемыми методом Джейка. Это означает, что в методе Джейка в неявной форме используется предположение о равновероятности всех исходных состояний системы.

Устойчивость и внутренняя непротиворечивость метода БФС апробированы на большом числе тестовых расчетов с использованием разработанной авторами компьютерной программы SpotCheck, являющейся реализацией метода БФС.

Для уменьшения необходимого объема выборочных проверок необходимо использование технических и организационных средств защиты состояния системы в промежутках между проведением проверок различного типа. Если принятые меры защиты достаточно эффективны, то состояние системы на уровне заданных в нормативной документации статистических критериев может быть проверено с помощью случайных выборок достаточно малых объемов.

Авторы

М.В. Горбатенко, к.ф.-м.н., А.М. Злобин, к.ф.-м.н., И.И. Сафронов, к.ф.-м.н., В.И. Юферев, к.ф.-м.н. (РФЯЦ-ВНИИЭФ)